Применение законов Кирхгофа для расчета разветвленных цепей
Применение законов Кирхгофа для расчета разветвленных цепей
Для расчета разветвленной электрической цепи произвольного вида существенной значение имеет число ветвей и узлов.
Ветвью электрической цепи называется такой участок, который состоит только из последовательно включенных источников напряжений и сопротивлений и вдоль которого в любой момент времени ток имеет одно и то же значение. Узлом электрической цепи называется место (точка) соединения трех и более ветвей.
При обходе по ветвям можно получить контур электрической цепи; каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям.
На рисунке 1 показана электрическая цепь пятью узлами и десятью ветвями. В частых случаях могут встретиться ветви только с сопротивлениями, без э.д.с. (ветвь 1-n) и с сопротивлениями практически равными нулю (ветвь 2-р)Так как напряжение на зажимах в ветви равно нулю (сопротивление равно нулю), то потенциалы точек 2 и р одинаковы и оба узла можно объединить в один узел.
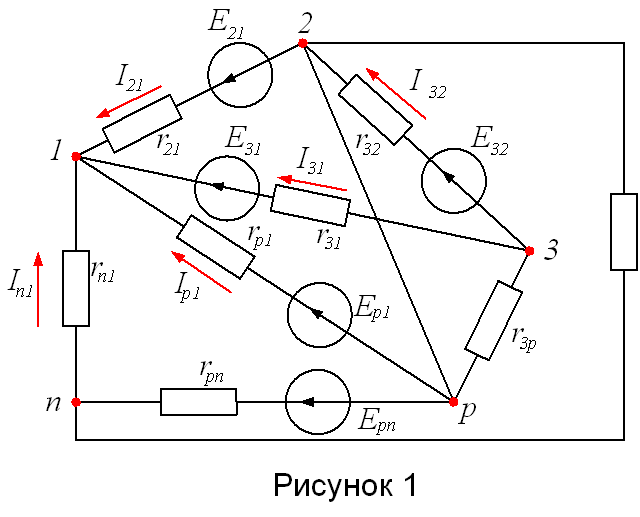
Режим электрической цепи произвольной конфигурации полностью определяется первым и вторым законами Кирхгофа.
Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равняется нулю, т.е.
![]() (1)
(1)
В этом уравнении одинаковые знаки должны быть взяты для токов, имеющих одинаковые положительные направления относительно узловой точки. В дальнейшем будем в уравнениях, составленных по первому закону Кирхгофа, записывать тока, которые направлены к узлу, с отрицательным знаками, а от узла – с положительным.
Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом контуре алгебраическая сумма э.д.с. равна алгебраической сумме напряжений на сопротивлениях, входящих в этот контур, т.е.
![]() (2)
(2)
В этом уравнении положительные знаки принимаются для токов и э.д.с., положительные направления которых совпадают с произвольно выбранным направление обхода рассматриваемого контура.
В теории электрических цепей решаются относительные задачи анализа электрических цепей, когда, например, известны конфигурация и элементы цепи, а требуется определить токи, напряжения и мощности тех или иных участков. К второму типу относятся обратные задачи, в которых, например, заданы токи и напряжения, а требуется найти конфигурацию цепи и выбрать ее элементы. Такие задачи называются задачами синтеза электрических цепей. Здесь много следует отметить, что решение задач анализа намного проще решения задач синтеза.
В практической электротехнике в настоящее время чаще встречаются задачи анализа, которые и будут в дальнейшем рассматриваться.
Задачи анализа могут быть решены при помощи законов Кирхгофа. Если известны все элементы цепи и ее конфигурация, а требуется определить токи, то при составлении уравнений по законам Кирхгофа рекомендуется придерживаться такой последовательности: сначала выбрать произвольные положительные направления токов во всех ветвях электрической цепи, затем составить уравнение ля узлов на основании закона Кирхгофа и, наконец, составить уравнение для контуров на основании второго закона Кирхгофа.
Пусть электрическая цепь содержит m ветвей и n узлов. Легко показать, что на основании первого и второго законов Кирхгофа можно составить соответственно (n-1) и (m-n+1) взаимно независимых уравнений, что в сумме дает необходимое число уравнений для определения m витков (во всех ветвях).
На основании первого закона Кирхгофа для n узлов (рисунок 1) можно записать n уравнений:
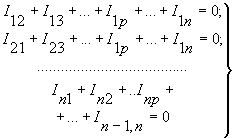 (3)
(3)
Так как любая ветвь связывает между собой только два узла , то ток каждой ветви должен обязательно войти в эти уравнения, причем 2 раза причем
![]() и т.д.
и т.д.
Следовательно сумма левых частей всех n уравнений дает тождественно нуль. Иначе говоря, одно из n уравнений может быть получено как следствие остальных (n-1) уравнений их число взаимно независимых уравнений, составленных на основании первого закона Кирхгофа , равно (n-1), т.е. на единицу меньше числа узлов. Например, для схемы (рисунок 2) с четырьмя узлами:
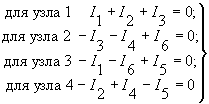 (4)
(4)
Суммируя эти уравнения, получим тождество: 0=0, следовательно, из этих четырех уравнений только три являются независимыми.
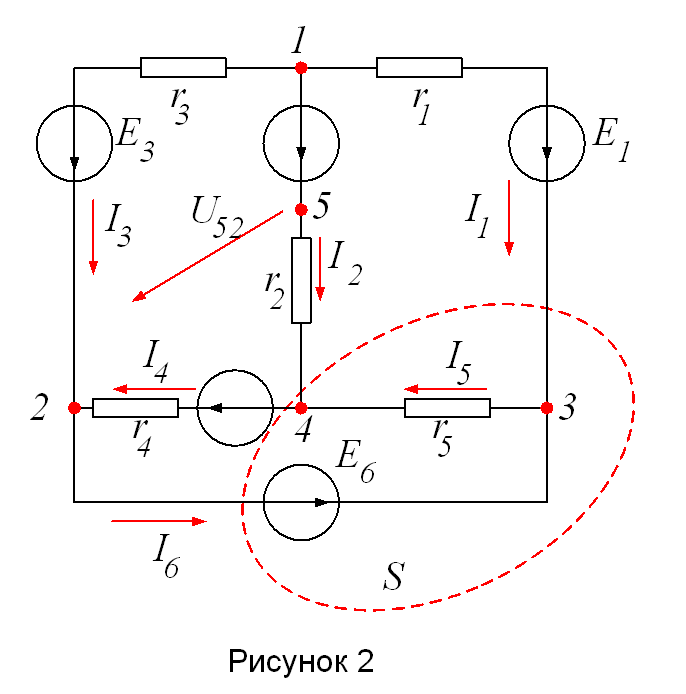
Так как беспредельное накопление электрических зарядов не может происходить как в отдельных узлах электрической цепи, так и в любых ее частях, ограниченных замкнутыми поверхностями, то первый закон Кирхгофа можно применить не только к какому-либо узлу, но и к любой замкнутой поверхности.
Например, для поверхности S (рисунок 2), как бы рассекающей электрическую схему на две части, справедливо уравнение ![]() , что можно также получить из уравнений 4 для узлов 3 и 4.
, что можно также получить из уравнений 4 для узлов 3 и 4.
Для того что бы установить число взаимно независимых уравнений, вытекающих из второго закона Кирхгофа, напишем для всех m ветвей схемы (рисунок 1) m уравнений на основании закона Ома:
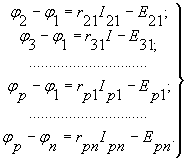 (5)
(5)
где ![]() - сопротивление ветви, соединяющей узлы р и n;
- сопротивление ветви, соединяющей узлы р и n;
![]() - суммарная э.д.с., действующая в ветви p-n в направлении от р к n;
- суммарная э.д.с., действующая в ветви p-n в направлении от р к n;
![]() и
и ![]() - потенциал узлов p и n.
- потенциал узлов p и n.
В этих уравнениях суммарное число неизвестных токов m ветвей и потенциалов n узлов равняется m+n.
В качестве примера напишем уравнение, связывающее потенциалы узлов с напряжениями и э.д.с., действующими в ветвях, для схемы (рисунок 2):
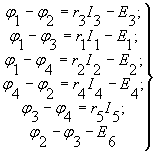 (6)
(6)
Складывая третье и четвертое уравнения и вычитая полученную сумму из первого, получаем:
![]() (7)
(7)
Если применить второй закон Кирхгофа к контуру 1-4-2-1 (при обходе вдоль контура по направлению движения часовой стрелки), то получается это же уравнение.
Аналогичным путем можно получить уравнение для остальных контуров:
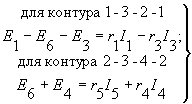 (8)
(8)
Современное решение любых трех уравнений (4) и уравнений (7) и (8)дает значение токов во всех ветвях электрической цепи, показанной на рисунке 2. Если в результате решения этих уравнений получается отрицательное значение для какого-либо тока, то это значит, что ее действительное направление противоположно принятому за положительное.
При составлении уравнений на основании второго закона Кирхгофа следует обращать особое внимание на то, чтобы получаемые уравнения были взаимно независимы. С этой целью необходимо выбирать контуры так, чтобы в них вошли все ветви схемы, а в каждый из контуров входило возможно меньшее число ветвей. При этом, если каждый новый контур, для которого составляется уравнение, имеет не меньше одного старой и одной новой ветви и не получается из контуров, для которых уже написаны уравнения, путем удаления из этих контуров общих ветвей, то такие контуры независимы.
Например, контур 1-3-4-2-1и (рисунок 2) можно получить из контуров 1-3-2-1 и 2-3-4-2 путем удаления ветви 2-3. Поэтому уравнение для контура 1-3-4-2-1 является следствием уравнений (8) и получается путем их суммирования.
Вторым законом Кирхгофа можно воспользоваться для определения напряжения между двумя произвольными точками схемы. В этом случае необходимо ввести в правую часть уравнений (5) искомое напряжение вдоль пути., как бы дополняющего незамкнутый контур до замкнутого. Например, для определения напряжения U52 (рисунок 2) можно написать уравнение для контура 2-1-5-2
![]()
или для конура 5-4-2-5
![]()
откуда легко найти искомое напряжение.
Для полной характеристики электрического цепи надо знать не только токи и напряжения, но также мощности источников и приемников энергии.
В замкнутой электрической цепи в соответствии с законом сохранения энергии развиваемая источниками энергии равна энергии, потребляемой приемниками. Из этого положения следует, что в любой электрической цепи алгебраическая сумма мощностей, развиваемая источниками э.д.с. , равна сумме мощностей, потребляемых всеми сопротивлениями (в том числе внутренними сопротивлениями источников энергии):
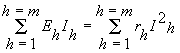 (9)
(9)
Если действительные напряжения э.д.с. и тока в некоторой ветви совпадают, то мощность такого источника э.д.с входит в уравнение (9) с положительным знаком, и источник отдает энергию в цепь (работает в режиме генератора). Если направления э.д.с. и тока в ветви противоположны, то мощность источника э.д.с. записываются уравнением (9) с отрицательным знаком, и такой источник работает в режиме приемника, потребляя энергию.
Необходимо отметить, что уравнение (9) может быть получено также из законов Кирхгофа.
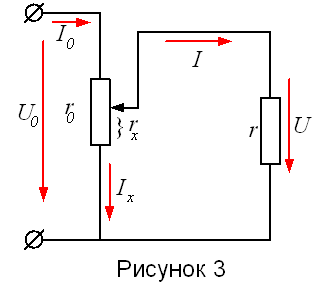
Пример 1. Для регулирования напряжения U на зажимах приемника с сопротивлением r=200 Ом включен делитель напряжения, полное сопротивление которого r0 = 1200 Ом (рисунок 3). Построить график изменения напряжения U в зависимости от сопротивления делителя rx при изменении его от нуля до r0 если U0=220 В.
Решение. На основании законов Кирхгофа можно написать для этой схемы следующие уравнения:
![]()
В результате совместного решения уравнений получается:
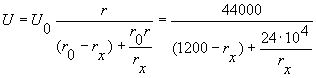
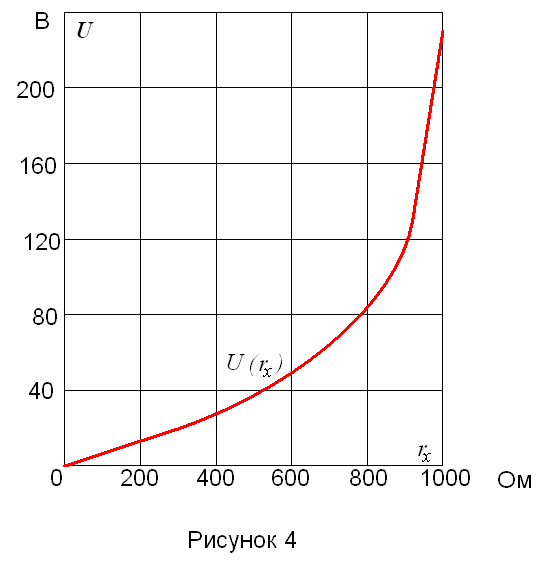
Подставляя числовые значения сопротивления rx , получим соответствующее значения напряжения U и строим график U(rx) (рисунок 4).
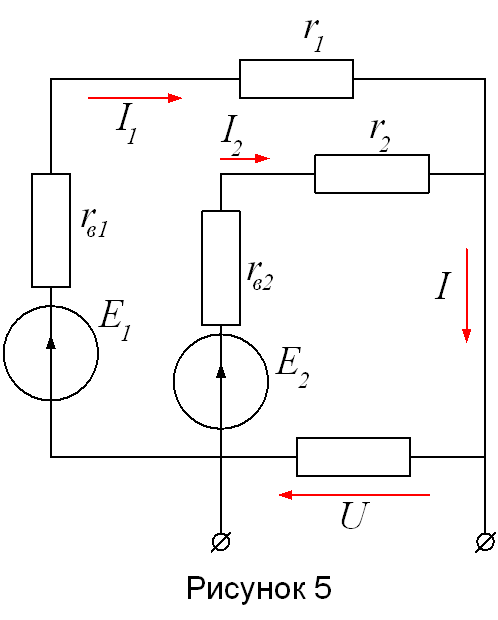
Пример 2. Для электрического суммирования величин иногда применяется схема, показанная на рисунке 5. Результирующая величина получается в виде напряжения U на сопротивлении r. Определить масштабный коэффициент, устанавливающий связь между напряжением U и суммой слагаемых величин, заданных в виде э.д.с. E1 и Е2.
Решение. На основании законов Кирхгофа можно написать для заданной схемы следующие уравнения:
![]()
![]()
![]()
В результате совместного решения этих уравнений получим:
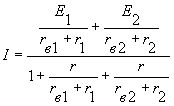
Если принять ![]() , то напряжение
, то напряжение
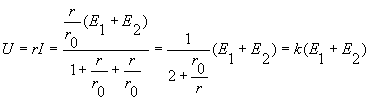
где ![]() - масштабный коэффициент.
- масштабный коэффициент.
Пример 3. Пользуясь законами Кирхгофа , написать два выражения для тока I0 в ветви с гальванометром рисунок 6, принимая в одном случае известным ток I, а в другом – напряжение U.
Решение. На основании законов Кирхгофа можно написать для заданной схемы с шестью неизвестными токами следующие уравнения:

В результате совместного решения этих уравнений получается выражение для тока I0 через U:
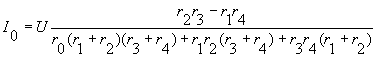
и через ток I:
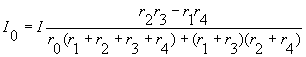
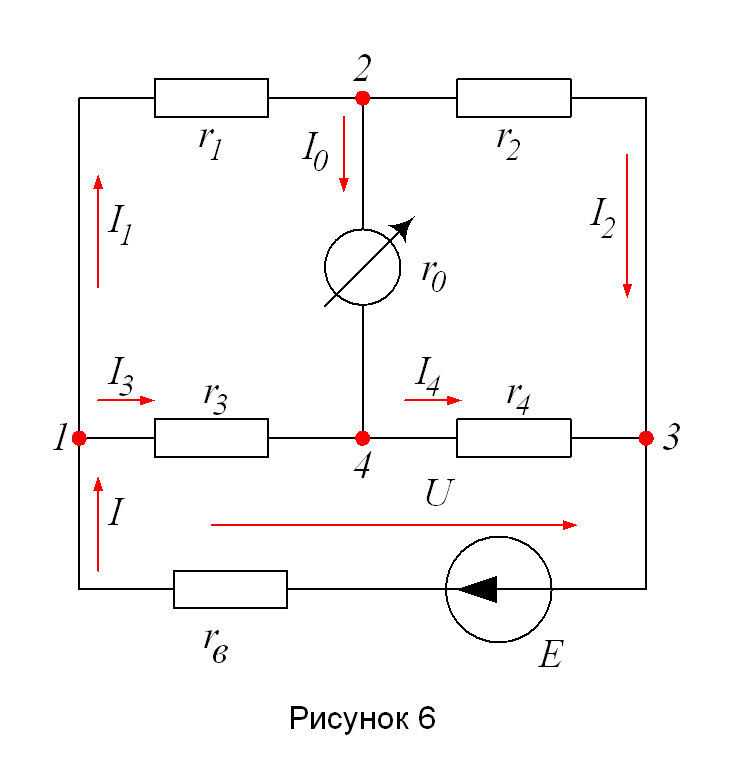
Пример 4. Какая будет допущена погрешность в определении тока в ветви с гальванометром (рисунок 6), если источник энергии заменить источником э.д.с. Е=12 В, rв=0,06 Ом, r1=r2=5 Ом, r3=10 Ом, r4=5 Ом и r0=10 Ом
Решение. Если пренебречь падением напряжения на внутреннем сопротивлении rв источника энергии, то напряжение U/ на зажимах 1-3 равно э.д.с. , т.е.
U/=Е=12 В.
Ток I/0 в ветви с гальванометром, так же как токи в остальных ветвях , возрастает в ![]() раз.
раз.
Из уравнений предыдущей задачи (пример №3)
U=11,88 B и I0 =0,125 А
Тогда
![]()
и
![]() т.е. погрешность равна около 1%.
т.е. погрешность равна около 1%.
