Как было указанно ранее, режим любой цепи полностью характеризуется уравнениями первого и второго законов Кирхгофа, причем для определения токов во всех m ветвях необходимо составить и решить систему уравнений с m неизвестными. Однако число уравнений, подлежащих решению, можно сократить, если воспользоваться методом узловых потенциалов , основанным на применении первого закона Кирхгофа и закона Ома.

Для выяснения сущности этого, метода рассмотрим, например, электрическую схему, показанную на рисунке 1.

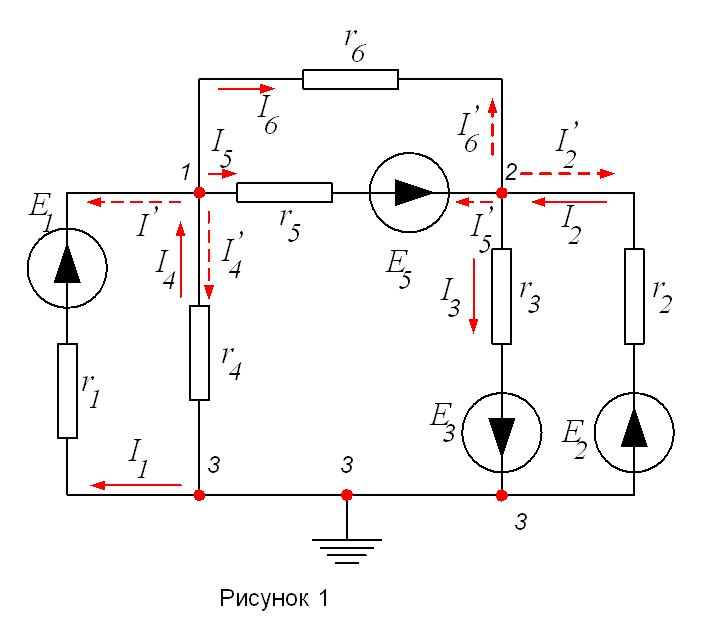
Пусть потенциал одного из узлов, например третьего узла, равен нулю, т.е. . Такое допущение не изменяет условий задачи, так как ток в каждой ветви зависит не от абсолютных значений потенциалов узлов, к которым присоединена ветвь, а от разности потенциалов на зажимах ветви.

На основании первого закона Кирхгофа для первого (1) и второго (2) узлов этой схемы при выбранных положительных направления токов получается:

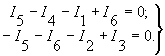(1)

Токи в ветвях на основании закона Ома

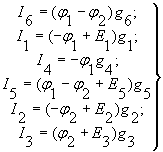(2)

где и - потенциалы первого и второго узлов.

После подстановки 2 в 1 и группировки членов получим:

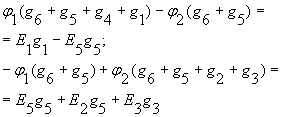
или

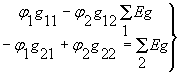(3)

В этих уравнениях - суммы проводимостей ветвей, присоединенных соответственно к первому и второму узлам; - сумма проводимостей ветвей соединяющих эти узлы.

Правая часть из уравнений (3) представляет собой алгебраическую сумму произведений э.д.с. источников на проводимости тех ветвей, которые присоединены к рассматриваемому узлу. Произведение вида Eg берется с положительным знаком в том случае, когда э.д.с. направлена к рассматриваемому узлц, и с отрицательным, когда э.д.с. направлены от узла.

Уравнение (3) не зависят от выбранных положительных направлений токов в ветвях.

Чтобы потвердеть это положение, рассмотрим опять схему, показанную на рисунке 1, и для каждого узла примем положительные направления токов от узла.

Для узлов 1 и 2 справедливы уравнения:

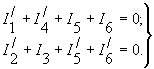(4)

Принимая как и раньше, , можно написать выражения для токов ветвей:

Для первого узла (1)

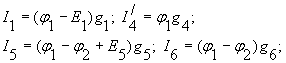
Для второго узла (2)

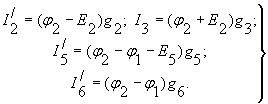(5)

После подстановки (5) в (4) и группировки слагаемых получаются уравнения совпадающие с (3).

Таким образом, можно написать уравнения для определения потенциалов узлов произвольной электрической цепи, исходя из ее конфигурации, не задаваясь положительными направлениями токов в ветвях; при этом потенциал одного из узлов надо принять равным нулю.

Если электрическая схема содержит не только источники э.д.с., но и источники тока, то в уравнения, составленные по первом закону Кирхгофа , войдут и токи источников вида (3) токи заданных источников тока учитывается для каждого узла в виде слагаемых в правой части, причем с положительными знаками должны быть взяты токи источников тока, направленные у узлу, а с отрицательными – от узла.

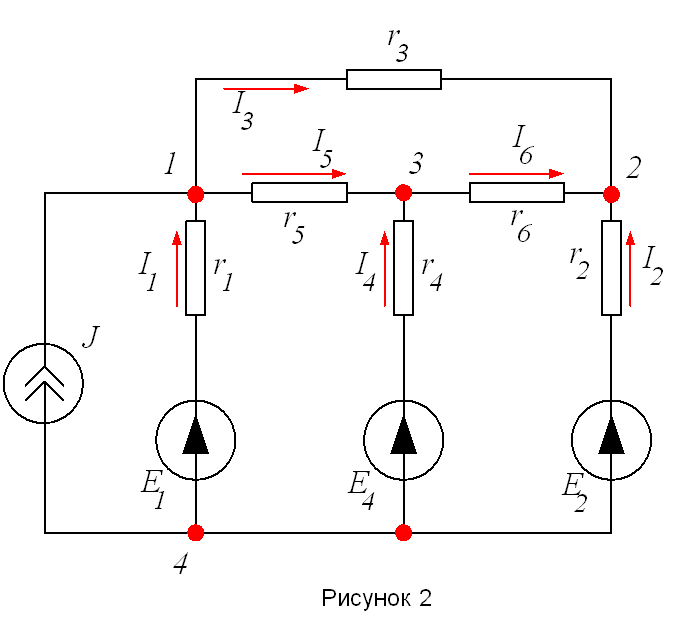
Например, для узлов 1,2 и 3 схемы, показанной на рисунке (2), при получим соответственно следующие уравнения:

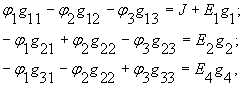
где

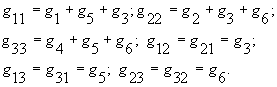
Если электрическая схема имеет в своем составе n+1 узлов (n- любое целое число), а потенциал, например (n+1) – го узла, принять равным нулю, то для определения n потенциалов остальных узлов получаются n уравнений:

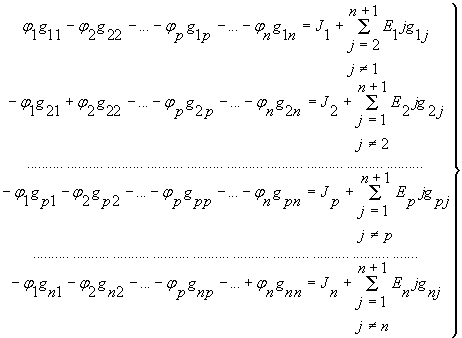(6)

или в более общей форме для любого p узла при

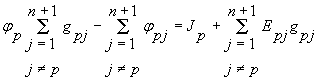(7)

В этих уравнениях, так же и в уравнениях (3), проводимость 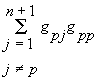(с двумя одинаковыми индексами) представляет собой суммарную проводимость ветвей, присоединенных к узлу p , а проводимость с двумя различными индексами равна сумме проводимостей ветвей, соединяющих между собой рассматриваемые узлы i и р. Правая часть каждого из уравнений содержит алгебраические суммы произведений э.д.с. на соответствующие проводимости для всех ветвей, присоединенных к узлу р, и узловой ток J_р , равный алгебраической сумме токов всех источников тока, присоединенных к тому же узлу.

При этом следует иметь в виду, что сумма всех узловых токов, как это вытекает из первого закона Кирхгофа, для замкнутых поверхностей всегда равна нулю. К узловым токам можно отнести и уже известные в каких-лидо ветвях токи. Проводимости таких ветвей в выражения вида g_pp и g_jp не входят.

Решив уравнения (6), можно определить потенциалы узлов, а зная потенциалы, легко найти токи во всех ветвях по закону Ома.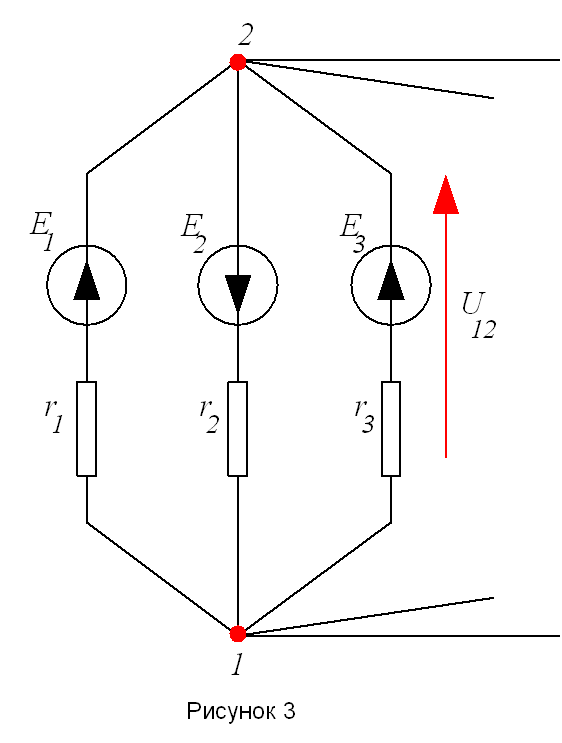

Пусть между двумя узлами 1 и 2 включено m ветвей (рисунок 3).Найдем напряжение U₁₂ . На основании уравнений (6) для первого узла получается уравнение

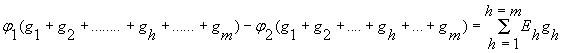(8)

откуда

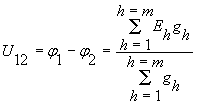(9)

где числитель представляет собой алгебраическую сумму произведений э.д.с. на проводимости соответствующих ветвей, содержащих э.д.с. (с положительным знаком берутся э.д.с ., направленные к узлу 1), а знаменатель – арифметическую сумму проводимостей всех ветвей, включенных между узлами.