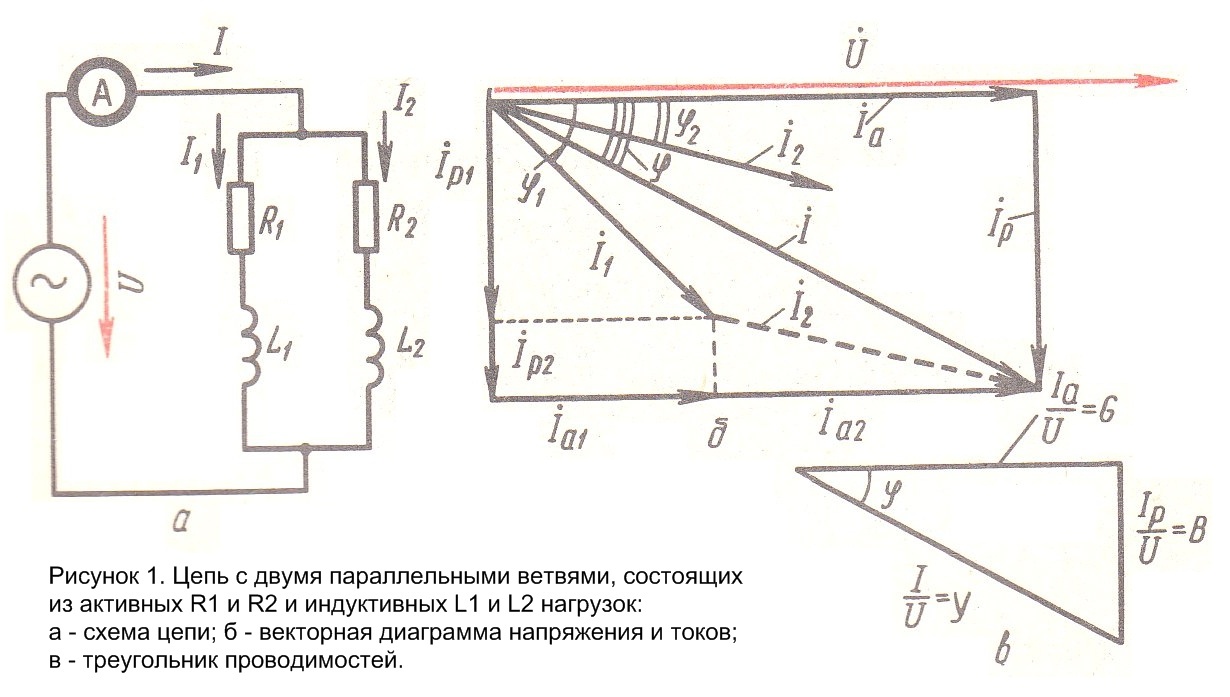
Рассмотрим цепь с двумя параллельными ветвями, в каждую из которых включен приемник энергии, обладающий активным и индуктивным сопротивлениями, - два двигателя, соответственно R₁ и L₁ и R₂ и L₂ (рисунок 1, а). Требуется найти общий ток I, потребляемый цепью, который представляет собой геометрическую сумму токов в ветвях I₁ и I₂.

В этой схеме напряжение U источника общее для обеих ветвей цепи, Поэтому векторную диаграмму начинаем строить с вектора напряжения . Затем угол , который можно определить по значению

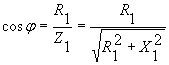
а сторону отставания (по часовой стрелке от вектора ), откладываем вектор тока . Аналогично под углом к откладываем вектор . Вектор общего тока определяем как геометрическую сумму векторов и . Проектируя векторы тока на горизонтальную ось (с ней совмещен вектор напряжения ), находим векторы активных токов и в ветвях с R₁ и R₂ и общий активный ток . На вертикальной оси получим соответственно реактивные токи ветвей и и общий реактивный ток

Из построенной диаграммы можно вывести следующие соотношения. Общий активный ток

(1)

Общий реактивный ток

(2)

Полный ток

(3)

Активная мощность, потребляемая всей схемой,

(4)

Этот метод расчета при большом расчете параллельных ветвей очень неудобен. Поэтому в подобных случаях пользуются методом проводимостей. Рассмотрим этот метод применительно к схеме на рисунке 1 (а).

Токи в первой и второй ветвях схемы могут быть определены как

и (5)

где и - полные сопротивления параллельных ветвей.

Величины, обратные полным сопротивлениям, то есть и , называют полными проводимостями и обозначают Y₁ и Y₂:

и или и .

Заменяя в формуле (5) величину Z величиной , получим :

и (6)

Активные составляющие этих токов

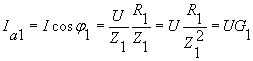(7)

и

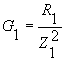где и 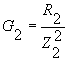- активные проводимости первой и второй ветвей.

Реактивные составляющие токов в первой и второй ветвях схемы

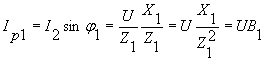и

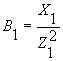где и 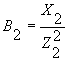- реактивные проводимости первой и второй ветвей.

Общие токи в ветвях

(8)

Сопоставляя формулы (8) и (7), можно заменить:

и (9)

то есть активная, реактивная и полная проводимости связаны между собой как стороны прямоугольного треугольника. Действительно, треугольник проводимостей (рисунок 1, в) можно получить из треугольника токов , и (рисунок 1, б), если каждую из его сторон разделить на общее напряжение U.

Продолжая расчет токов в схеме, показанной на рисунке 1 (а), получим активную и реактивную составляющую общего тока:

где и - соответственно активная и реактивная проводимости всей цепи.

Общий ток может быть найден как

(10)

где - полная проводимость всей цепи.

Активную Р, реактивную Q и полную S мощности всей цепи можно определить как

(11)

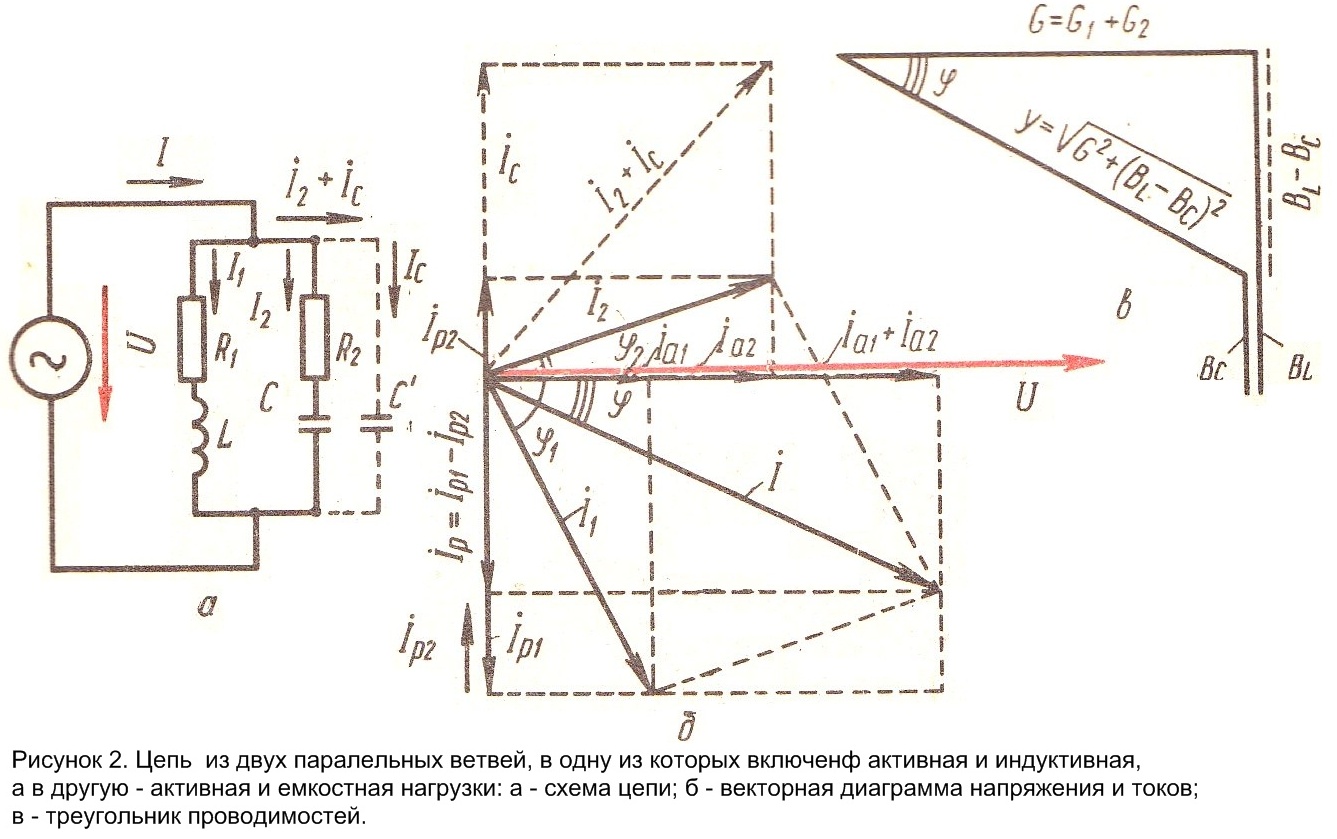
Рассмотрим теперь случай параллельного соединения двух ветвей (рисунок 2, а), в одну из которых включены активное сопротивление и индуктивность, а в другую – активное сопротивление и емкость.

Векторную диаграмму следует начинать строить с векторам напряжения . Затем определить следует и , причем будет отстающим (в цепь включена индуктивность), а - опережающим (в цепь включена емкость):

;

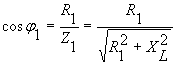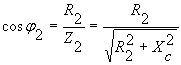
По значениям и определяют углы и , затем под этим углами к напряжению откладывают соответствующие им векторы токов и . Векторы общего тока в цепи равен геометрической сумме векторов токов и .

Как видно, из векторной диаграммы, общий ток

где - реактивный ток в общей ветви.

Выделив на общей диаграмме (рисунок 2, б) треугольник токов , и и поделив их на общее для них напряжение U, получим треугольник проводимостей ,,(рисунок 2,в), в котором -реактивная проводимость ветвей с индуктивностью; - реактивная проводимость с емкостью.

Из этого треугольника следует, что

то есть полная проводимость равна корню квадратному из суммы квадратов результирующих активных и реактивных проводимостей. Общий ток в неразветвленном участке

(11)

Угол сдвига тока относительно напряжения может быть найден из треугольника проводимостей по значению тангенса:

Рассмотрим случай, когда , и угол . Практически этого можно достигнуть, если первым двум ветвям дополнительно подключить конденсатор (рисунок 2, а) такой емкости, чтобы сила емкостного тока в новой ветви .Тогда реактивный, индуктивный индуктипроцессвный и реактивный емкостной токи полностью скомпенсируют друг друга. В общей ветви, как видно из векторной диаграммы, будет протекать только ток

,

то есть лишь активный ток.

Из формулы (11) общий ток

Явление, которое возникает в подобном случае, носит название резонанса токов. При резонансе токов оказываются равными реактивные индукционная Q_L и емкостная Q_C мощности, так как

и

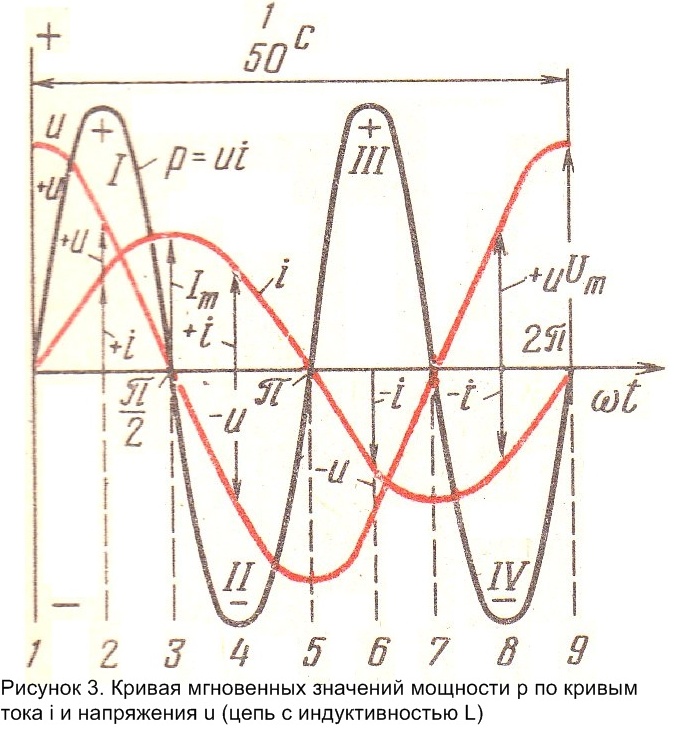
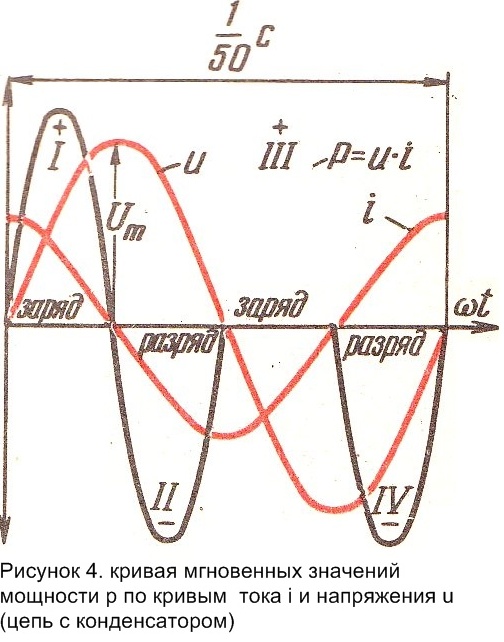
Из рисунков 3 и 4 видно, что в отрезке времени, когда мгновенное напряжение возрастает от нуля до максимального как положительного, так и отрицательного значений, мгновенная мощность в цепи с индуктивностью (рисунок 3, полупериоды II и IV)имеет отрицательное значение , а в цепи с емкостью (рисунок 4, полупериоды I и III) – положительное значение, то есть цепь с индуктивностью в этот момент отдает энергию в сеть, а цепь с индуктивностью потребляет энергию, поскольку конденсаторы заряжаются.

Таким образом, при резонансе токов наблюдается колебательный процесс перехода энергии магнитного поля индуктивности в энергию электрического поля конденсатора и обратно, а энергия от источника расходуется только в сопротивлениях R₁ и R₂.

Явление компенсации реактивного тока используют для улучшения (компенсации) коэффициента мощности в электроустановках.