С изменением напряжения на обкладках конденсатора, включенного в цепь переменного тока (рисунок 1 а), изменяется его заряд. Приращение заряда , который поступает в конденсатор за очень малый промежуток времени , равно произведению силы тока i в данный момент времени на единицу времени :

(1)

Но, как рассматривалось выше,

(2)

где q – электрический разряд конденсатора, Кл; С – емкость конденсатора, Ф; u – напряжение на обкладках конденсатора, В.

Из выражения 2 следует, что приращение заряда при увеличении напряжения на обкладках конденсатора на будет равно

(3)

Согласно формулам 1 и 2

или

(4)

то есть переменный ток в цепи с емкостью пропорционален скорости изменения приложенного к конденсатору напряжения.

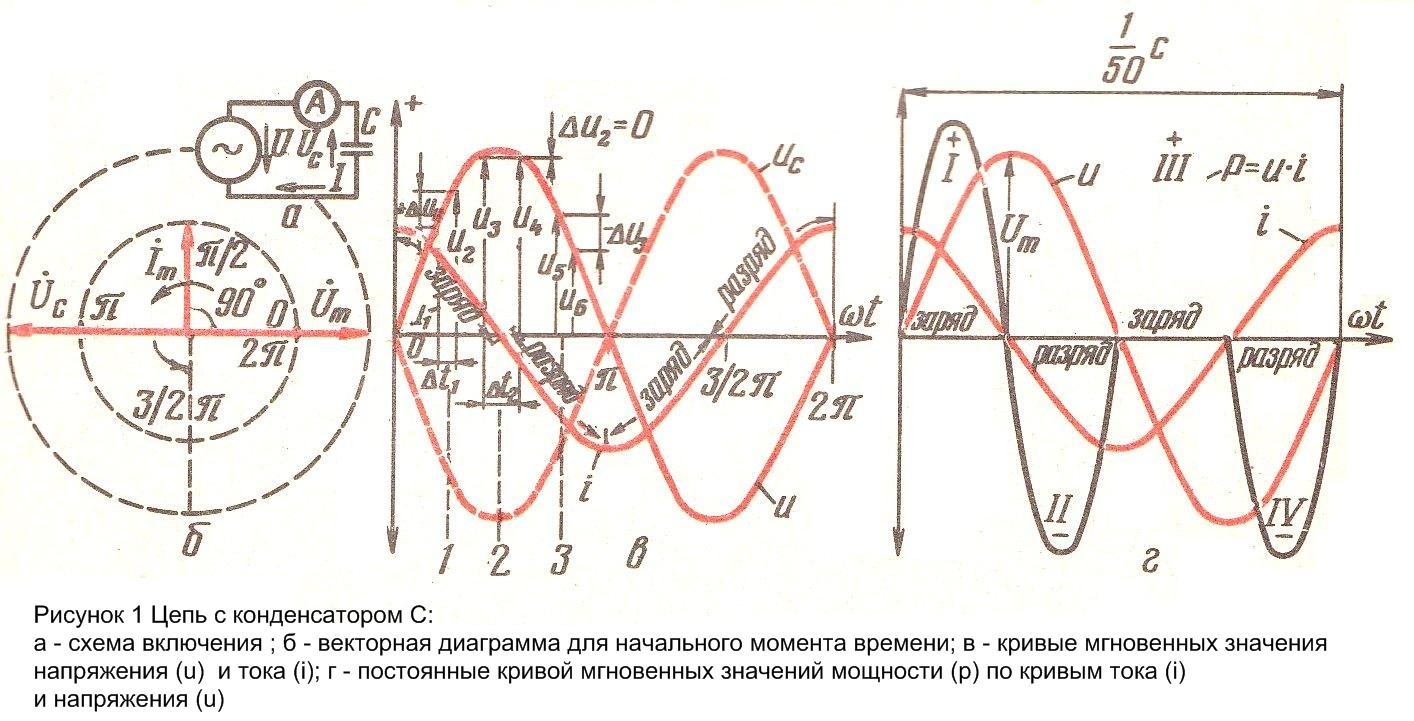
Пользуясь формулой 4 и учитывая, что цепь включена на синусоидальное напряжение , можно построить кривую мгновенных значений тока (рисунок 1 в).В первую четверть периода приращение напряжения имеет положительный знак. Например, для момента времени 1: . В соответствии с формулой 4 мгновенное значение тока в этот момент времени также имеет положительный знак. В момент времени также равен нулю: , то есть кривая тока в момент времени 2 проходит через нуль. Конденсатор при этом обладает максимальным зарядом. В момент времени 3 приращение напряжения имеет отрицательный знак, так как оно нарастает в отрицательном направлении: . Ток для этого момента времени также отрицателен:

Рассуждая подобный образом, исследуют процесс в каждый момент времени.

Для любого момента времени напряжение и ток могут быть подсчитаны как

;

(5)

Чтобы получить соотношение между действующими значениями тока и напряжения в цепи с емкостью, в формуле 4 необходимо раскрыть величину

Пусть в момент времени t мгновенное значение напряжения , тогда для момента времени мгновенное напряжение

Отсюда

Поскольку

и , то

,

откуда

(6)

Подставляя в формулу 4 вместо его значение из формулы 6, получим:

(7)

Следовательно, ток в цепи с емкостью опережает напряжение на 90⁰ , или радиан. Векторная диаграмма для начального момента времени представлено на рисунке 1 (б).

Теперь проследим процесс зарядки и разрядки конденсатора. Если в первую четверть периода конденсатора заряжается, то во вторую четверть периода, когда напряжение уменьшается от максимального значения до нуля, конденсатор разряжается и посылает ток навстречу приложенному напряжению. Когда напряжение проходит через нуль, ток в цепи достигает своего максимального значения. С момента перехода напряжения через нуль вновь начинается процесс заряда конденсатора, ток постепенно убывает. В момент, когда напряжение, достигнув своего максимального отрицательного значения, начинает уменьшаться, конденсатор, полностью зарядившись, начинает разряжаться.

Из формул 5 и 7 имеем:

Поделим обе части равенства на :

,

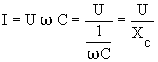или (8)

где I – действующее значение силы тока, А; U – действующее значение напряжения, В; С – емкость конденсатора, Ф; - угловая частота тока, рад/с; - реактивное емкостное сопротивление конденсатора.

Емкостное сопротивление обратно пропорционально частоте напряжения, приложенного к конденсатору, и емкости конденсатора, то есть чем больше частота и чем больше емкость конденсатора, тем меньше значение емкостного сопротивления (и наоборот). Размерность этого сопротивления

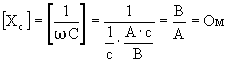
Емкостное сопротивление носит реактивный характер: в моменты, когда мгновенное значение напряжения увеличивается, конденсатор запасает заряд (заряжается), напряжение на его обкладках повышается. При уменьшении мгновенных значений напряжения конденсатор разряжается и отдает запасенный заряд обратно генератору.

Пример 1. Определить силу тока в цепи с конденсатором С = 10 мкФ (10 ∙ 10^-6 Ф), если частота переменного тока f = 50 Гц, а напряжение U = 220 B.

Решение. Емкостное сопротивление

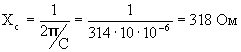
Сила тока в цепи

Мгновенная мощность в каждый момент времени

(9)

Следовательно, мгновенная мощность – синусоидальная величина, изменяющаяся с двойной частотой по сравнению с частотой тока (напряжения).Кривую мгновенных значений этой мощности можно построить графическим путем. Рассматривая полученную развернутую диаграмму мощности (рисунок 1, г), можно отметить следующие. Мгновенная мощность, как и в цепи с индуктивностью, колеблется с двойной частотой. В полупериоды I и III мгновенная мощность имеет продолжительный знак (а при индуктивности - отрицательный). Фактически смысл этого явления заключается в том, что в эти полупериоды конденсатор заряжается – ток совпадает по направлению с напряжение (по знаку). В конденсаторе запасается энергия электрического поля:

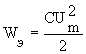(10)

где С-емкость конденсатора, Ф; U_m – максимальное значение напряжения, приложенного к конденсатору, В.

В полупериоды II и IV, когда напряжение уменьшается от максимального значения до нуля, конденсатор разряжается, отдавая запасенную энергию обратно генератору. Энергия, полученная цепью с конденсатором от генератора за период , равна нулю. Мощность, которая характеризует эту энергию, является реактивной:

(11)

Как всякую реактивную мощность, ее измеряют в вольт-амперах реактивных (ВАР).

Реактивная энергия как в цепи с индуктивностью, так и в цепи с емкостною циркулирует между источником тока и токоприемником, на выделяясь и не превращаясь в другие формы энергии на индуктивном или емкостном сопротивлении, но реактивный ток нагружает линию и вызывает в ней потери на нагрев проводов.