Цепь переменного тока с активной и индуктивной нагрузкой
treugoma.ru › Учебник › Однофазные цепи переменного синусоидального тока ›
Цепь переменного тока с активной и индуктивной нагрузкой
Реальная катушка индуктивности обычно имеет и активное сопротивление, которым нельзя пренебречь. На рисунке 1 “а” показана цепь катушки индуктивность которой L, а активное сопротивление R. на рисунке 1 “б” изображены кривые мгновенных значений напряжения u и тока i в цепи R и L, а на рисунке 1 “в” - взаимное расположение векторов напряжения Um и тока Im, сдвинутых относительно один другого на угол ![]() .
.
Если в цепи с R и L проходит синусоидальный ток ![]() , то мгновенное значение активной составляющей напряжения может быть определено как
, то мгновенное значение активной составляющей напряжения может быть определено как ![]() . Мгновенное значение напряжения на индуктивном сопротивлении в соответствии с формулой
. Мгновенное значение напряжения на индуктивном сопротивлении в соответствии с формулой
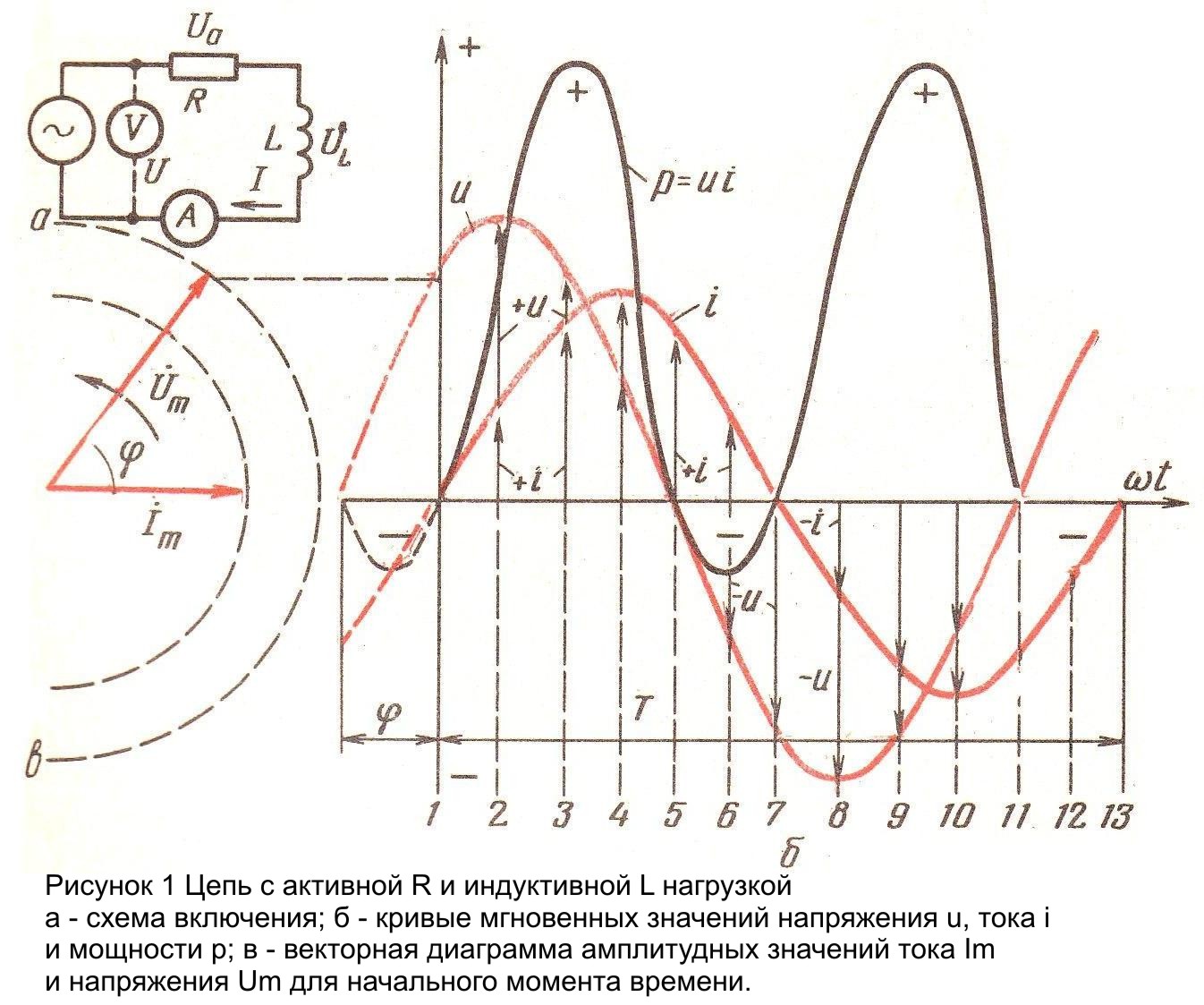
Мгновенное же значение напряжения, приложенного ко всей цепи, равно алгебраической сумме мгновенных значений напряжений на активном и индуктивном сопротивлениях:
Так как оба слагаемых этой суммы – синусоидальные величины, изменяющиеся с одинаковой частотой ω, то результирующее напряжение uтоже синусоидально и имеет ту же частоту.
Это результирующее напряжениеu представлено на рисунке 1 “б”. Векторная диаграмма амплитудных значений напряжения и тока приведена на рисунке “в”.
Анализ схем с несколькими сопротивлениями в цепи удобно проводить на векторных диаграммах действующих значений величин, которые могут быть измерены приборами, например вольтметром и амперметром (рисунок 1 “а”). Для перехода к диаграмме амплитудных величин каждый вектор действующего значения следует увеличивать в ![]() раз, так как
раз, так как ![]() , а
, а ![]() .
.
Порядок построения векторной диаграммы для схемы 1 “а” таков. Общим для обоих сопротивлений R и XL в этой схеме является ток, действующее значение которого измеряют амперметром А. Откладываем этот ток в определенном, удобном для нас, масштабе (рисунок 1 “а”) по горизонтали, так как начальная фаза тока i=Imsin ω t равна нулю (рисунок 1 “б”). Напряжение Ua совпадает по фазе с током, поскольку оно приложено у участку цепи, имеющему только активное сопротивление R. Поэтому вектор ![]() совпадает по фазе с током, поскольку оно приложено к участку цепи, имеющему только активное сопротивление R. Поэтому
совпадает по фазе с током, поскольку оно приложено к участку цепи, имеющему только активное сопротивление R. Поэтому ![]() откладываем вдоль вектора
откладываем вдоль вектора ![]() .Масштаб напряжения также выбираем удобным для построения . Например если для тока мы приняли масштаб 1:1, то есть 1 ампер отложим в 1 см длины вектора
.Масштаб напряжения также выбираем удобным для построения . Например если для тока мы приняли масштаб 1:1, то есть 1 ампер отложим в 1 см длины вектора ![]() , то для напряжения удобнее принять масштаб 100:1, то есть 100 вольт отложить в 1 см.
, то для напряжения удобнее принять масштаб 100:1, то есть 100 вольт отложить в 1 см.
Напряжение ![]() опережает ток I по фазе на угол
опережает ток I по фазе на угол ![]() , так как оно приложено к участку цепи, имеющему только индуктивное сопротивление. Поэтому вектор
, так как оно приложено к участку цепи, имеющему только индуктивное сопротивление. Поэтому вектор ![]() отложим в направлении, перпендикулярном вектору
отложим в направлении, перпендикулярном вектору ![]() . Причем масштаб вектора
. Причем масштаб вектора ![]() должен быть равен масштабу
должен быть равен масштабу ![]() . Складывая затем геометрический
. Складывая затем геометрический ![]() и
и ![]() , получим вектор действующего значения общего напряжения
, получим вектор действующего значения общего напряжения ![]() , приложенного к цепи с R и XL.
, приложенного к цепи с R и XL.
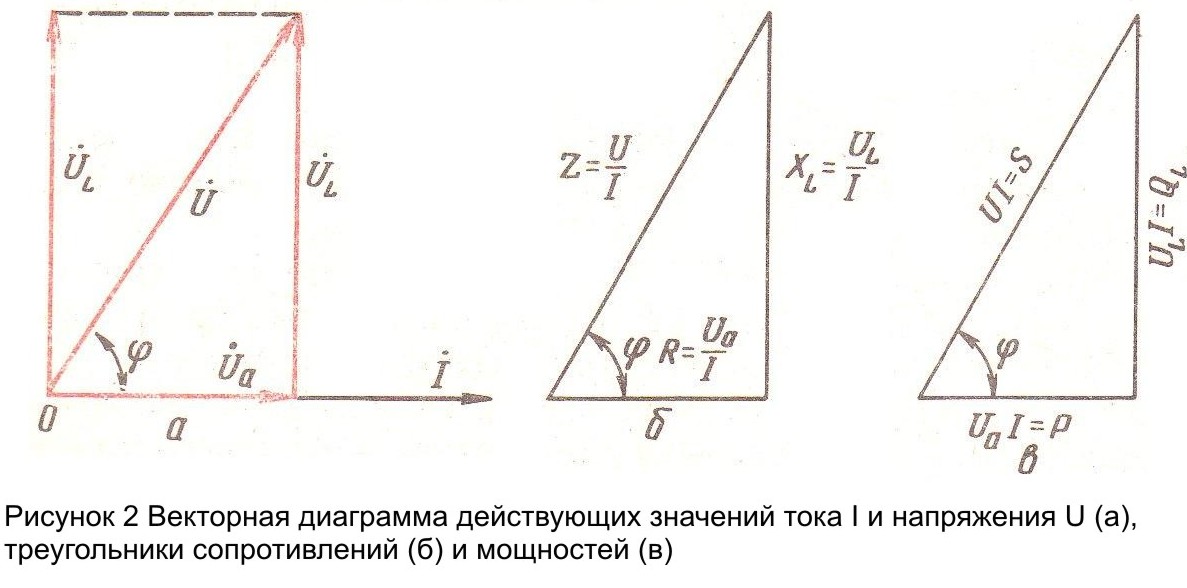
На векторной диаграмме (рисунок 2 “а”) векторы ![]() ,
, ![]() и
и ![]() образуют прямоугольный треугольник называют треугольником напряжений.
образуют прямоугольный треугольник называют треугольником напряжений.
По теореме Пифагора для этого треугольника:
Если все стороны треугольника напряжения разделить на величину Iто получиться так называемый треугольник сопротивлений (рисунок 2 “б”). Из этого треугольника
Если известно напряжение U, приложенное к к исследуемой цепи (оно может быть измерено вольтметром Vна рисунке 1 “а”), а также ток в цепи I (он измеряется амперметром А), то полное сопротивление всей цепи
отсюда
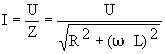 (5)
(5)
Формула 5 является математическим выражением закона Ома для индуктивной и активной нагрузкой, с последовательным соединением индуктивного и резисторного элементов .
Пользуясь векторными диаграммами, можно написать следующие соотношения между составляющими напряжения и найти значение угла ![]() . Так, из рисунка 2 “а”
. Так, из рисунка 2 “а”
Из треугольника сопротивлений
В цепи с параллельным включением активного и индуктивного сопротивления аналогично уравнению 6:
![]() (8)
(8)
Пример 1. Определить полное сопротивление, ток и угол сдвига фаз между напряжением сети и током в цепи, если активное сопротивление цепи R=50 Ом, индуктивность катушки, включенной последовательно с активным сопротивлением, L=0,5 Г, частота тока f= 50 Гц, напряжение U=220 В.
Решение. Индуктивное сопротивление
Полное сопротивление
Ток в цепи
Угол сдвига фаз находим следующим образом:
График мгновенных значений мощности, которую потребляет цель с активным сопротивлениями, можно получить способом, изложенным при рассмотрении цепи с активным сопротивлением. С этой целью для ряда моментов времени (1,2,….13) определяют мгновенные значения тока i и напряжения u (рисунок 1 “б”), а затем перемножив их, находя мгновенные значения р. Расчет сводят в таблицу.
Таблица 1 Данные для графического построения мгновенных значений u,I и p=ui
| Точки (рисунок 1) | Значение амплитуд, мм | ||
| Напряжения u | Тока i | Мощности p | |
| 1 | +23 | 0 | 0 |
| 2 | +26 | +8 | +19 |
| 3 | +23 | +17,5 | +40 |
| 4 | +14 | +20 | +28 |
| 5 | 0 | +17,5 | 0 |
| 6 | -14 | +8 | -11 |
| 7 | -23 | 0 | 0 |
| 8 | -26 | -8 | +19 |
| 9 | -23 | -17,5 | +40 |
| 10 | -14 | -20 | +28 |
| 11 | 0 | -17,5 | 0 |
| 12 | +14 | -8 | -11 |
По полученным точкам строят развернутую диаграмму мощности, приняв масштаб для ее построения, в 7 раз большей, чем для построения u.
Как видно из полученной диаграммы, мощность не является синусоидальной величиной. Значению энергии за период времени Т соответствует площадь, заключенная между кривой мощности и осью времени. В отрезке времени 5-7 и 11-13 энергия имеет отрицательное значение и должна быть отнесена к энергии, которая возвращается из магнитного поля катушки в сеть (к генератору). Энергия, соответствующая площади ограниченной кривой поступает из генератора в цепь. Разность энергии со знаком плюс и минус равняется активной энергии, необратимость расходуемой на активном сопротивлении цепи.
Мгновенное значение мощности в цепи с активным и индуктивным сопротивлениями можно также определить аналитически:
![]()
![]()
![]()
Второй член полученного выражения описывается периодической кривой, изменяющейся с двойной частотой по сравнению с частотой тока и напряжения. Как было показано в статье “Действующее значение переменного тока”, при таком характере кривой ее среднее значение за период равно нулю.
Поэтому, переходя к средним значениям, получим среднюю мощность цепь, которую называют ее активной мощностью:
Характер мощностей и соотношение между ними в схеме с активными и индуктивными сопротивлениями можно установить, если все стороны треугольника напряжений умножить на действующее значение тока I. При этом образуется треугольник мощностей (рисунок 1, в).Из этого треугольника активная мощность, измеряется, как известно, в “Ватах” (Вт) или “Киловатах” (кВт),
![]() (10),
(10),
то есть результат тот же что и при аналитическом определении.
Реактивная мощность, измеряемая в “вольт-амперах реактивных” (ВАР) или “киловольт-амперах реактивных” (кВАР),
Полная мощность
Полную мощность измеряют в “Вольт-амперах” (![]() ) или “киловольт - амперах” (
) или “киловольт - амперах” (![]() ).
).
Косинус фи (![]() ) в цепи с индуктивностью в практике часто называют отстающим или положительным.
) в цепи с индуктивностью в практике часто называют отстающим или положительным.
На активном сопротивлении выделяется активная мощность ![]() , а индуктивное сопротивление определяется значение реактивной мощности, как
, а индуктивное сопротивление определяется значение реактивной мощности, как
В практике активную мощность измеряют ваттметром, а полную мощность подсчитывают как произведение показаний вольтметра и амперметра. Зная эти две величины, можно рассчитывать реактивную мощность.
Величину ![]() называется также коэффициентом мощности. Практически в электроустановках
называется также коэффициентом мощности. Практически в электроустановках ![]() определяют, пользуясь показаниями ваттметра (или счетчика с пересчетом киловатт-часов в киловатты), вольтметра и амперметра, или измеряют специальным прибором фазометром. Отношение показаний ваттметра к произведению показаний вольтметра на показания амперметра дает значение коэффициента мощности:
определяют, пользуясь показаниями ваттметра (или счетчика с пересчетом киловатт-часов в киловатты), вольтметра и амперметра, или измеряют специальным прибором фазометром. Отношение показаний ваттметра к произведению показаний вольтметра на показания амперметра дает значение коэффициента мощности:
Пример 2: Однофазный электрический двигатель, коэффициент полезного действия которого ![]() , потребляет из сети напряжением
, потребляет из сети напряжением ![]() с
с ![]() , ток
, ток ![]() . Определить потребляемую из сети активную мощность
. Определить потребляемую из сети активную мощность ![]() ; полезную мощность
; полезную мощность ![]() двигателя; циркулирующую в сети реактивную мощность
двигателя; циркулирующую в сети реактивную мощность ![]() ;полную мощность
;полную мощность ![]() .
.
Решение:
Активная мощность, потребляемая двигателем из сети,
Полезная мощность двигателя:
Реактивная мощность:
Полная мощность:
или иначе:
Пример 3: Ваттметр показывает 1500 Вт, а вольтметр – 380 В, амперметр – 50 А. Определить ![]() , реактивную мощность, активный и реактивный токи.
, реактивную мощность, активный и реактивный токи.
Решение:
Коэффициент мощности
Реактивная мощность
где
Активный ток:
Реактивный ток:
